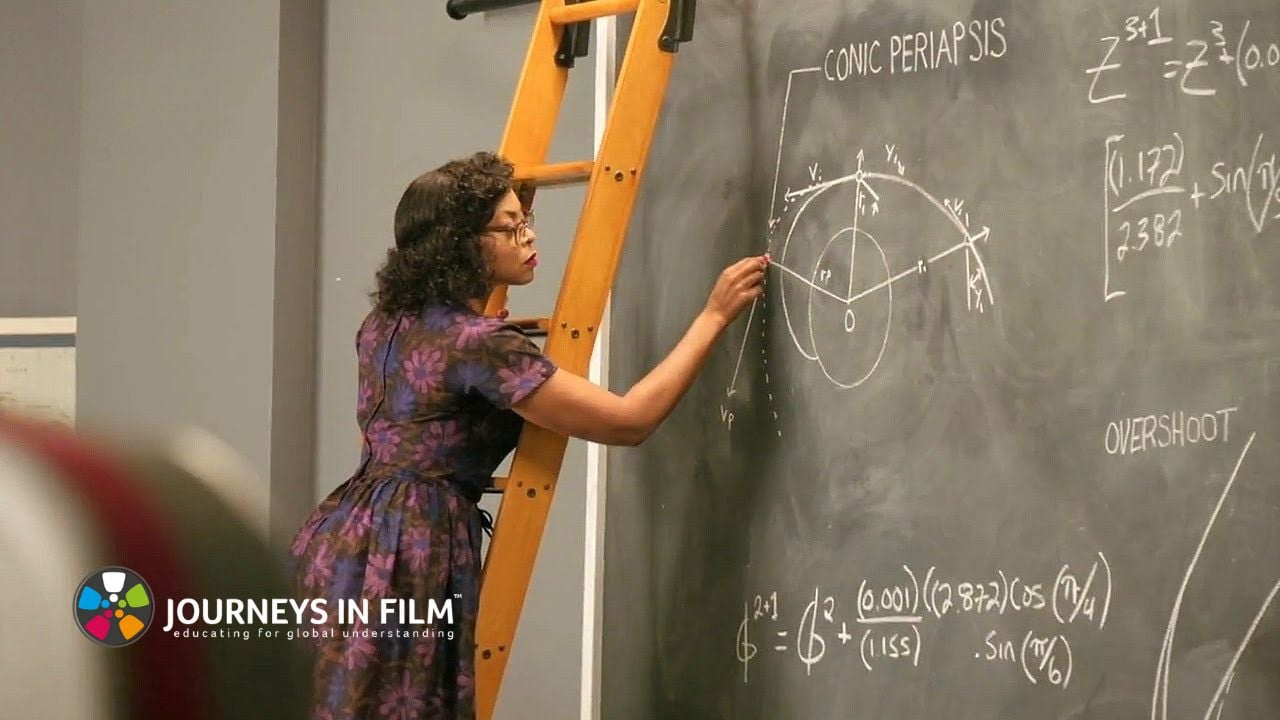About This Lesson
Check out this fun science and math lesson that uses Disney's Hidden Figures to support learning!
This lesson gives students the opportunity to strengthen their skills in both calculating orbits and managing huge numbers.
Mathematics is at the heart of the film Hidden Figures. It is mathematics that supports the ambitions of the three principal characters, mathematics that fills their days in West Computing, and mathematics that brings John Glenn and later astronauts back from their missions. Calculating orbits was particularly important, and so was the ability to handle immensely large numbers in a manageable way.
This lesson begins with an investigation of calculations that involve exponents, and from there leads students to apply those rules to calculations involving large numbers. Students will see the need for scientific notation when dealing with astronomical distances and develop an intuitive understanding of the notation through several mental arithmetic exercises. Exponential arithmetic and scientific notation are together in the same lesson in order to highlight the connections between the two.
The first part of the lesson is a sequence of problems that lead the students through some (but not all) of the calculation rules for exponential expressions. Scientific notation is nominally a middle school standard in most schools. However, discomfort with exponents, and in particular with scientific notation, is widespread at all ages.
The second part of the lesson is designed as a “from firstprinciples” investigation of ellipses and how they relate to German mathematician and astronomer Johannes Kepler’s first and second laws. The goal in many cases is not to construct a mathematical proof of the claims made, but only to examine why they might be reasonable. The problems in part two are designed for class discussion, with the students presenting their own work and critiquing that of others.
It’s amazing that some shapes you can draw on a piece of paper are able to describe the motion of planets through space with unerring accuracy. We hope this lesson can help you convey how amazing and exciting that is to your students!
This includes 2 handouts:
- Problems on Scientific Notation
- Problems on Conic Sections
This lesson features a class discussion activity. We recommend the Journeys in Film Group Discussion Facilitation Guidelines to support these discussions.
Learn more about teaching with Hidden Figures across the curriculum with the Journeys in Film Hidden Figures Curriculum Guide.